It is a truth universally acknowledged, that a couple in possession of good fortune, must be in want of enhanced intimate pleasure. Among the various accoutrements designed for the boudoir that might benefit both parties simultaneously, the vibrating cock ring distinguishes itself as particularly versatile and approachable. Whether one seeks to prolong one's stamina, improve the quality of one's tumescence, or introduce delightful vibrations to one's most private moments, these diminutive contrivances yield remarkable results. Having devoted considerable time to the examination of the superior options available for purchase, I find myself exceedingly eager to impart all necessary intelligence regarding the selection and employment of these pleasure-enhancing devices.
What Exactly Is a Vibrating Cock Ring?
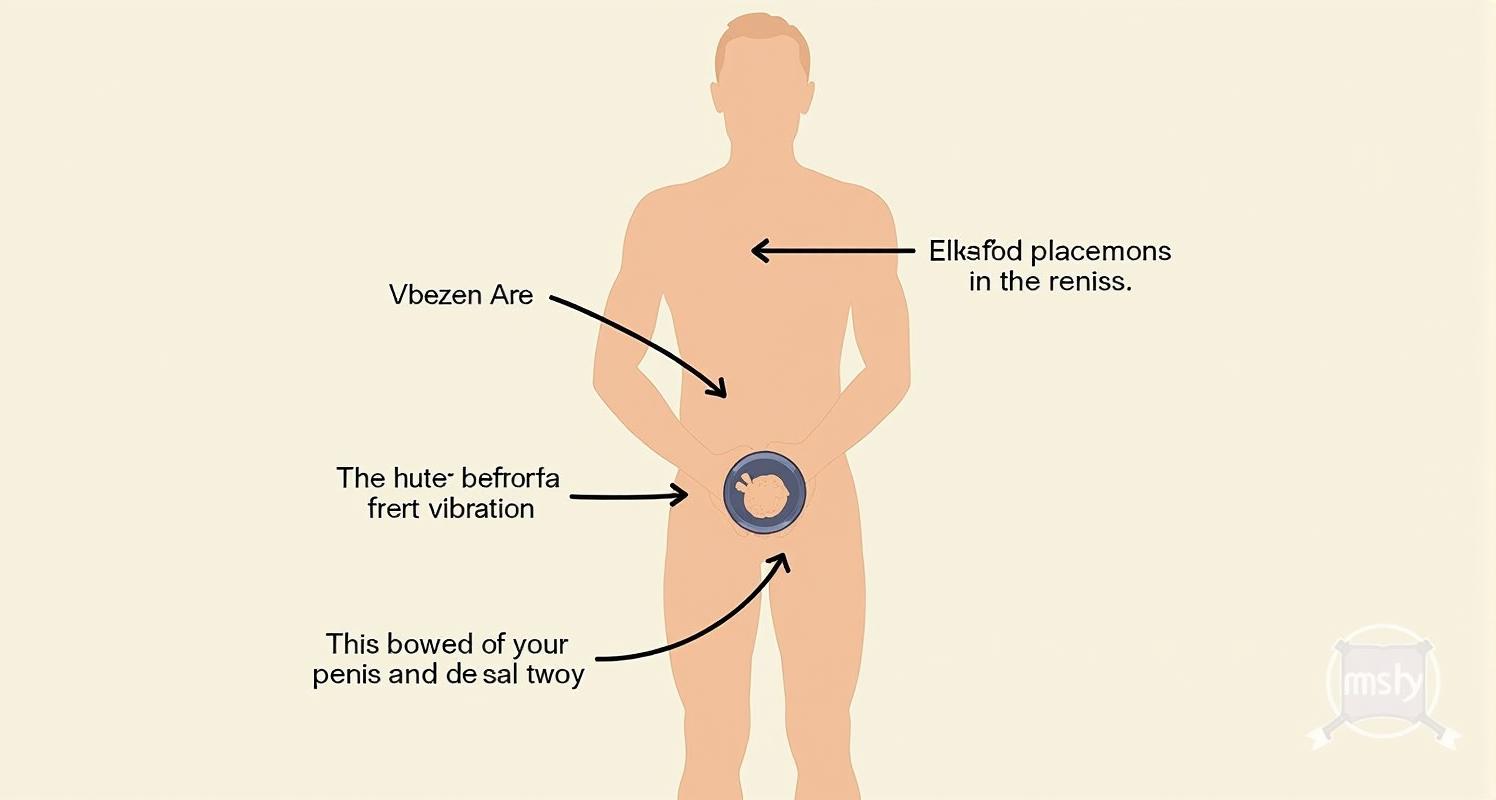
The vibrating cock ring presents itself as nothing more complex than the standard cock ring with the addition of a vibrating mechanism. In its fundamental design, it comprises an elastic circlet that encircles the base of the male member (or indeed both the member and the testicles, depending upon the particular style) with an attached vibrating component. This vibrating element is customarily positioned to stimulate both participants during their congress.
I recollect with perfect clarity my first encounter with such an item in a shop—I experienced simultaneous curiosity and a slight trepidation. However, upon acquiring further knowledge, I came to understand that these are, in fact, among the most accessible implements of pleasure available to the discerning couple.
Benefits of Using a Vibrating Cock Ring
Before proceeding to specific recommendations, one must consider the advantages that might induce one to place such an item upon one's bedside table:
- Enhanced erection quality - Through the gentle impediment of blood flowing outward from the male organ, cock rings may assist in maintaining firmer erections
- Extended playtime - A great many gentlemen report increased longevity when employing a cock ring
- Dual stimulation - The vibrating mechanism provides pleasurable sensations for both participants
- Ease of use - No intricate techniques are requisite—one need only apply it and commence
- Economical introduction - When compared with numerous other intimate toys, quality vibrating cock rings remain relatively affordable
How to Use a Vibrating Cock Ring
One of the most frequently posed inquiries I encounter is merely: how does one employ these contraptions? Allow me to elucidate.
Basic Application
- Begin with lubrication - Apply a modest quantity of water-based lubricant to the interior of the ring and the gentleman's appendage
- Select your position - Determine whether the ring shall encircle merely the shaft or both the shaft and testicles
- Apply when partially tumescent - It is generally less taxing to don when not fully aroused
- Position the vibrator - Ensure the vibrating element is situated where it shall make contact with the desired areas during intercourse
- Activate the mechanism - Most examples feature simple single-button operation
- Adjust as necessary - One should not hesitate to reposition during use to discover the optimal location
Safety Tips
I cannot emphasize with sufficient vigor: one must not wear a cock ring for periods exceeding 20-30 minutes. Should one experience any numbness, coldness, or discomfort, remove it forthwith. Furthermore, one must always cleanse one's toy thoroughly betwixt uses with mild soap and warm water or a specialized cleanser.

Do Vibrating Cock Rings Actually Work? Reddit Weighs In
I devoted some time to perusing Reddit discussions to ascertain what actual users pronounce on the subject of vibrating cock rings. The general consensus? They are indeed efficacious—though expectations must be tempered.
One Reddit correspondent remarked: "My wife initially harbored skepticism but now declares it her favorite toy. The vibrations strike her most agreeably, and I maintain my ardor considerably longer with it applied."
Another shared this intelligence: "While it shall not utterly transform one's amorous life, it introduces an element of diversion and unquestionably assists me in maintaining greater firmness for extended periods. The thirty dollars I expended were well invested."
The most common favorable observations centered around: - Enhanced clitoral stimulation for female companions - Increased endurance for the gentleman - The novelty factor introducing excitement
Common criticisms included: - Certain models producing feeble vibrations - Battery longevity issues in less expensive models - Discovering the proper fit may require patience and experimentation
Do Cock Rings with Vibration Help the Female Partner?
This constitutes another frequently posed question, and the answer is an emphatic affirmative—when utilized correctly. The vibrating component is typically situated to make contact with the clitoris during penetrative congress, providing stimulation that might otherwise be absent.
What renders this particularly effective is that it permits consistent clitoral stimulation without interrupting the natural rhythm of intercourse or requiring a hand to maintain a separate vibrator in position. Numerous ladies report that this consistent stimulation renders climax during penetrative congress considerably more attainable.
One must bear in mind that positioning is of paramount importance. What proves perfectly suitable for one couple might prove wholly inadequate for another, thus one must be prepared to adjust and communicate regarding what produces the most agreeable sensations.
Top Vibrating Cock Rings Worth Considering
Having researched numerous options and perused countless testimonials, I have assembled this comparison of some of the finest vibrating cock rings presently available:
| Model | Best For | Battery Life | Material | Special Features | Price Range |
|---|---|---|---|---|---|
| We-Vibe Pivot | Couples seeking premium quality | 2 hours | Body-safe silicone | App-controlled, waterproof | $90-120 |
| Lovehoney Basics Vibrating Ring | Novices with limited means | 30-40 minutes | Stretchy TPE | Simple single-speed operation | $10-15 |
| Lelo Tor 2 | Those seeking luxury | 1.5 hours | Premium silicone | 6 vibration patterns, fully waterproof | $110-140 |
| Tenga SVR | Versatility | 40 minutes | Medical-grade silicone | May be employed as a standalone massager | $60-80 |
| Screaming O Charged OWow | Enthusiasts of power | 1 hour | Silicone | Powerful motor, rechargeable | $40-60 |
How to Choose the Right Vibrating Cock Ring
With such an abundance of options available, how might one select the most appropriate? Here are the factors I consider most significant:
Material Matters
I invariably recommend body-safe silicone for vibrating cock rings. It is non-porous, simple to cleanse, and possesses sufficient elasticity to ensure comfort while maintaining adequate tension. One should avoid materials resembling jelly, which may contain phthalates and other potentially harmful chemical compounds.
Size and Fit
While most vibrating cock rings stretch to accommodate different dimensions, if one is particularly well-endowed or of modest size, one must attend to the dimensions. Some manufacturers offer various sizes, while others produce one-size-suits-most. When in doubt, a slightly more elastic option is generally preferable to one that might prove excessively constrictive.
Vibration Settings
Basic models offer a single vibration speed, whereas more sophisticated options provide multiple patterns and intensities. As a general principle, multiple settings afford greater flexibility to discover what proves most effective for oneself and one's companion.
Battery Type
Rechargeable models demand greater initial expenditure but economize on money and inconvenience in the long term. Single-use battery models are typically less dear but consider the ongoing expense of replacements. Should one opt for a rechargeable model, verify the battery life—nothing so thoroughly dispels amorous sentiment as a toy ceasing to function mid-engagement.
How to Wear a Vibrating Cock Ring
There exist several methods of wearing a vibrating cock ring, depending upon the design and one's personal preference:
The Basic Position
The most common approach is to slide the ring around the base of the penis shaft, with the vibrating element positioned atop to make contact with one's partner's clitoris during the missionary position or similar arrangements.
The Full Package
Some gentlemen prefer wearing the ring around both the penis and testicles. This provides a more intense sensation and may further delay emission. To accomplish this: 1. Stretch the ring with one's fingers 2. Carefully insert one testicle at a time through the ring 3. Follow with the penis (while partially tumescent) 4. Position the vibrating element as desired
The Double Ring
Certain models feature two rings—one for the shaft and one for the testicles. These provide maximum restriction and sensation but may prove somewhat more complicated to don.
I personally find the basic position most suitable for novices, while the full package option may be explored once one has grown comfortable with the sensation of wearing a cock ring.
Creative Ways to Use Your Vibrating Cock Ring
While the standard application proves satisfactory, there exist other methods to enjoy one's vibrating cock ring:
- Solo play enhancer - Wear it during self-gratification for a different sensation
- Non-penetrative play - Employ it during preliminary amorous activities as a handheld vibrator
- Different positions - Attempt it in positions where your bodies align differently—you might discover new areas of pleasure
- Perineum stimulation - Some models can be positioned to stimulate the perineum as well
Cleaning and Maintenance
To maintain one's vibrating cock ring in optimal condition:
- Always cleanse before and after use with mild soap and warm water
- Dry completely before storage
- Store in a cool, dry location away from direct sunlight
- Remove batteries from non-rechargeable models during extended periods of disuse
- Examine regularly for any tears or damage
Are Vibrating Cock Rings Worth It?
After all this research and personal experience, I can declare with confidence that vibrating cock rings offer excellent value for couples wishing to enhance their intimate experiences. They are relatively inexpensive compared to many intimate toys, simple to use, and provide benefits for both participants.
That said, they are not miraculous solutions. Like any aid to amorous congress, they function best when accompanied by good communication, a spirit of adventure, and realistic expectations. They complement good sexual chemistry rather than create it.
The Bottom Line
Vibrating cock rings represent one of the most accessible entries into the realm of couples' intimate toys. They combine the erection-enhancing benefits of traditional cock rings with the added pleasure of vibration, creating a mutually beneficial arrangement for both parties.
Whether one seeks to add additional stimulation, maintain stronger erections, or simply attempt something novel together, a quality vibrating cock ring constitutes a worthwhile addition to one's intimate collection.
Remember that the best results arise from open communication with one's partner regarding what produces pleasure and what does not. One should not fear to experiment with different positions and settings until discovering what best suits one's unique physiology and preferences.
Have you employed a vibrating cock ring previously? Are you contemplating adding one to your collection of intimate accessories? The journey toward enhanced pleasure often involves exploration and discovering what works specifically for you and your partner.

